

In mathematics, when something satisfies certain properties, we often ask if other things satisfy the same properties. Before investigating this, we will give names to these properties.
Let \(A\) be nonempty set and let \(R\) be a relation on \(A\).
Before exploring examples, for each of these properties, it is a good idea to understand what it means to say that a relation does not satisfy the property. So let \(A\) be a nonempty set and let \(R\) be a relation on \(A\).
Let \(a, b \in \mathbb\) and let \(n \in \mathbb\). If \(a \equiv b\) (mod \(n\)), then \(b \equiv a\) (mod \(n\)).
In Section 7.1, we used directed graphs, or digraphs, to represent relations on finite sets. Three properties of relations were introduced in Preview Activity \(\PageIndex\) and will be repeated in the following descriptions of how these properties can be visualized on a directed graph.
Let \(A\) be a nonempty set and let R be a relation on \(A\).


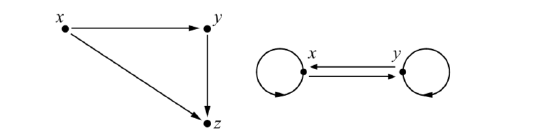
Let \(A = \\) and let \(R\) be the following relation on \(A\):
Draw a directed graph for the relation \(R\) and then determine if the relation \(R\) is reflexive on \(A\), if the relation \(R\) is symmetric, and if the relation \(R\) is transitive.
Answer
Add texts here. Do not delete this text first.
In mathematics, as in real life, it is often convenient to think of two different things as being essentially the same. For example, when you go to a store to buy a cold soft drink, the cans of soft drinks in the cooler are often sorted by brand and type of soft drink. The Coca Colas are grouped together, the Pepsi Colas are grouped together, the Dr. Peppers are grouped together, and so on. When we choose a particular can of one type of soft drink, we are assuming that all the cans are essentially the same. Even though the specific cans of one type of soft drink are physically different, it makes no difference which can we choose. In doing this, we are saying that the cans of one type of soft drink are equivalent, and we are using the mathematical notion of an equivalence relation.
An equivalence relation on a set is a relation with a certain combination of properties that allow us to sort the elements of the set into certain classes. In this section, we will focus on the properties that define an equivalence relation, and in the next section, we will see how these properties allow us to sort or partition the elements of the set into certain classes.
Let \(A\) be a nonempty set. A relation \(\sim\) on the set \(A\) is an equivalence relation provided that \(\sim\) is reflexive, symmetric, and transitive. For \(a, b \in A\), if \(\sim\) is an equivalence relation on \(A\) and \(a\) \(\sim\) \(b\), we say that \(a\) is equivalent to \(b\).
Most of the examples we have studied so far have involved a relation on a small finite set. For these examples, it was convenient to use a directed graph to represent the relation. It is now time to look at some other type of examples, which may prove to be more interesting. In these examples, keep in mind that there is a subtle difference between the reflexive property and the other two properties. The reflexive property states that some ordered pairs actually belong to the relation \(R\), or some elements of \(A\) are related. The reflexive property has a universal quantifier and, hence, we must prove that for all \(x \in A\), \(x\ R\ x\). Symmetry and transitivity, on the other hand, are defined by conditional sentences. We often use a direct proof for these properties, and so we start by assuming the hypothesis and then showing that the conclusion must follow from the hypothesis.
Let \(M\) be the relation on \(\mathbb\) defined as follows:
For \(a, b \in \mathbb\), \(a\ M\ b\) if and only if \(a\) is a multiple of \(b\).
So \(a\ M\ b\) if and only if there exists a \(k \in \mathbb\) such that \(a = bk\).
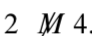 So there exist integers \(x\) and \(y\) such that \(x\ M\ y\) but
So there exist integers \(x\) and \(y\) such that \(x\ M\ y\) but 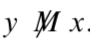 Hence, the relation \(M\) is not symmetric.
Hence, the relation \(M\) is not symmetric.The relation \(M\) is reflexive on \(\mathbb\) and is transitive, but since \(M\) is not symmetric, it is not an equivalence relation on \(\mathbb\).
Solution
Define the relation \(\sim\) on \(\mathbb\) as follows: For all \(a, b \in Q\), \(a\) \(\sim\) \(b\) if and only if \(a - b \in \mathbb\). For example:
To prove that \(\sim\) is reflexive on \(\mathbb\), we note that for all \(q \in \mathbb\), \(a - a = 0\). Since \(0 \in \mathbb\), we conclude that \(a\) \(\sim\) \(a\). Now prove that the relation \(\sim\) is symmetric and transitive, and hence, that \(\sim\) is an equivalence relation on \(\mathbb\).
Answer
Add texts here. Do not delete this text first.
One of the important equivalence relations we will study in detail is that of congruence modulo \(n\). We reviewed this relation in Preview Activity \(\PageIndex\).
Theorem 3.30 tells us that congruence modulo n is an equivalence relation on \(\mathbb\). Recall that by the Division Algorithm, if \(a \in \mathbb\), then there exist unique integers \(q\) and \(r\) such that
\(a = nq + r\) and \(0 \le r < n\).
Theorem 3.31 and Corollary 3.32 then tell us that \(a \equiv r\) (mod \(n\)). That is, a is congruent modulo n to its remainder \(r\) when it is divided by \(n\). When we use the term “remainder” in this context, we always mean the remainder \(r\) with \(0 \le r < n\) that is guaranteed by the Division Algorithm. We can use this idea to prove the following theorem.
Let \(n \in \mathbb\) and let \(a, b \in \mathbb\). Then \(a \equiv b\) (mod \(n\)) if and only if \(a\) and \(b\) have the same remainder when divided by \(n\).
Proof
Let \(n \in \mathbb\) and let \(a, b \in \mathbb\). We will first prove that if \(a\) and \(b\) have the same remainder when divided by \(n\), then \(a \equiv b\) (mod \(n\)). So assume that a and bhave the same remainder when divided by \(n\), and let \(r\) be this common remainder. Then, by Theorem 3.31,
\(a \equiv r\) (mod \(n\)) and \(b \equiv r\) (mod \(n\)).
Since congruence modulo \(n\) is an equivalence relation, it is a symmetric relation. Hence, since \(b \equiv r\) (mod \(n\)), we can conclude that \(r \equiv b\) (mod \(n\)). Combining this with the fact that \(a \equiv r\) (mod \(n\)), we now have
\(a \equiv r\) (mod \(n\)) and \(r \equiv b\) (mod \(n\))
We can now use the transitive property to conclude that \(a \equiv b\) (mod \(n\)). This proves that if \(a\) and \(b\) have the same remainder when divided by \(n\), then \(a \equiv b\) (mod \(n\)).
We will now prove that if \(a \equiv b\) (mod \(n\)), then \(a\) and \(b\) have the same remainder when divided by \(n\). Assume that \(a \equiv b\) (mod \(n\)), and let \(r\) be the least nonnegative remainder when \(b\) is divided by \(n\). Then \(0 \le r < n\) and, by Theorem 3.31,
\(b \equiv r\) (mod \(n\)).
Now, using the facts that \(a \equiv b\) (mod \(n\)) and \(b \equiv r\) (mod \(n\)), we can use the transitive property to conclude that
\(a \equiv r\) (mod \(n\))
This means that there exists an integer \(q\) such that \(a - r = nq\) or that
We will prove that the relation ~ is an equivalence relation on \(\mathbb\). The relation \(\sim\) is reflexive on \(\mathbb\) since for each \(a \in \mathbb\), \(a - a = 0 = 2 \cdot 0 \cdot \pi\).
Now, let \(a, b \in \mathbb\) and assume that \(a\) \(\sim\) \(b\). We will prove that \(b\) \(\sim\) \(a\). Since \(a\) \(\sim\) \(b\), there exists an integer \(k\) such that
\[a - b = 2k\pi.\]
By multiplying both side of this equation by -1, we obtain
\[\begin <(-1)(a - b)>&= & <(-1)(2k\pi)>\\ &= & <2(-k)\pi.>\end\]
Since \(-k \in \mathbb\), the last equation proves that \(b\) \(\sim\) \(a\). Hence, we have proven that if \(a\) \(\sim\) \(b\), then \(b\) \(\sim\) \(a\) and, therefore, the relation \(\sim\) is symmetric.
Let \(U\) be a finite, nonempty set and let \(\mathcal(U)\) be the power set of \(U\). Recall that \(\mathcal(U)\) consists of all subsets of \(U\). (See page 222.) Define the relation \(\approx\) on \(\mathcal(U)\) as follows:
For \(A, B \in P(U)\), \(A \approx B\) if and only if card(\(A\)) = card(\(B\)).
For the definition of the cardinality of a finite set, see page 223. This relation states that two subsets of \(U\) are equivalent provided that they have the same number of elements. Prove that \(\approx\) is an equivalence relation on
Answer
Add texts here. Do not delete this text first.
\(\bullet\) For \(a, b \in Z\), \(a \sim b\) if and only if 2 divides \(a + b\).
\(\bullet\) For \(a, b \in Z\), \(a \approx b\) if and only if 3 divides \(a + b\).
\(\bullet\) For \(a, b \in Z\), \(a \sim b\) if and only if \(2a + 3b \equiv 0\) (mod 5).
\(\bullet\) For \(a, b \in Z\), \(a \approx b\) if and only if \(a + 3b \equiv 0\) (mod 5).
\(\bullet\) For \(a, b \in Z\), \(a \sim b\) if and only if \(xy \ge 0\).
\(\bullet\) For \(a, b \in Z\), \(a \approx b\) if and only if \(xy \le 0\).
Proposition. Let \(R\) be a relation on a set \(A\). If \(R\) is symmetric and transitive, then \(R\) is reflexive. Proof Let \(x, y \in A\). If \(x\ R\ y\), then \(y\ R\ x\) since \(R\) is symmetric. Now, \(x\ R\ y\) and \(y\ R\ x\), and since \(R\) is transitive, we can conclude that \(x\ R\ x\). Therefore, \(R\) is reflexive.
Proposition. Let \(\sim\) be a relation on \(\mathbb\) where for all \(a, b \in \mathbb\), \(a \sim b\) if and only if \((a + 2b) \equiv 0\) (mod 3). The relation \(\sim\) is an equivalence relation on \(\mathbb\). Proof Assume \(a \sim a\). Then \((a + 2a) \equiv 0\) (mod 3) since \((3a) \equiv 0\) (mod 3). Therefore, \(\sim\) is reflexive on \(\mathbb\). In addition, if \(a \sim b\), then \((a + 2b) \equiv 0\) (mod 3), and if we multiply both sides of this congruence by 2, we get \[\begin <2(a + 2b)>&\equiv & > \\ <(2a + 4b)>&\equiv & > \\ <(a + 2b)>&\equiv & > \\ <(b + 2a)>&\equiv & .> \end\] This means that \(b\ \sim\ a\) and hence, \(\sim\) is symmetric. We now assume that \((a + 2b) \equiv 0\) (mod 3) and \((b + 2c) \equiv 0\) (mod 3). By adding the corresponding sides of these two congruences, we obtain \[\begin <(a + 2b) + (b + 2c)>&\equiv & > \\ <(a + 3b + 2c)>&\equiv & > \\ <(a + 2c)>&\equiv & .> \end\] Hence, the relation \(\sim\) is transitive and we have proved that \(\sim\) is an equivalence relation on \(\mathbb\).
Explorations and Activities
17. Other Types of Relations. In this section, we focused on the properties of a relation that are part of the definition of an equivalence relation. However, there are other properties of relations that are of importance. We will study two of these properties in this activity.
A relation \(R\) on a set \(A\) is a circular relation provided that for all \(x\), \(y\), and \(z\) in \(A\), if \(x\ R\ y\) and \(y\ R\ z\), then \(z\ R\ x\).
(a) Carefully explain what it means to say that a relation \(R\) on a set \(A\) is not circular.
(b) Let \(A = \\). Draw a directed graph of a relation on \(A\) that is circular and draw a directed graph of a relation on \(A\) that is not circular.
(c) Let \(A = \\). Draw a directed graph of a relation on \(A\) that is circular and not transitive and draw a directed graph of a relation on \(A\) that is transitive and not circular.
(d) Prove the following proposition:
A relation \(R\) on a set \(A\) is an equivalence relation if and only if it is reflexive and circular.
A relation \(R\) on a set \(A\) is an antisymmetric relation provided that for all \(x, y \in A\), if \(x\ R\ y\) and \(y\ R\ x\), then \(x = y\).
(e) Carefully explain what it means to say that a relation on a set \(A\) is not antisymmetric.
(f) Let \(A = \\). Draw a directed graph of a relation on \(A\) that is antisymmetric and draw a directed graph of a relation on \(A\) that is not antisymmetric.
(g)Are the following propositions true or false? Justify all conclusions.
Add texts here. Do not delete this text first.
This page titled 7.2: Equivalence Relations is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by Ted Sundstrom (ScholarWorks @Grand Valley State University) via source content that was edited to the style and standards of the LibreTexts platform.